그래프 이론과 그래프 탐색 알고리즘(Graph Theory and Graph Search Algorithm)
Graph theory
branch of mathematics concerned with networks of points connected by lines. 그래프 이론은 선으로 연결된 점들의 네트워크와 관련된 수학의 한 분야이다.
쾨니히스베르크 다리 건너기 문제(Königsberg bridge problem)
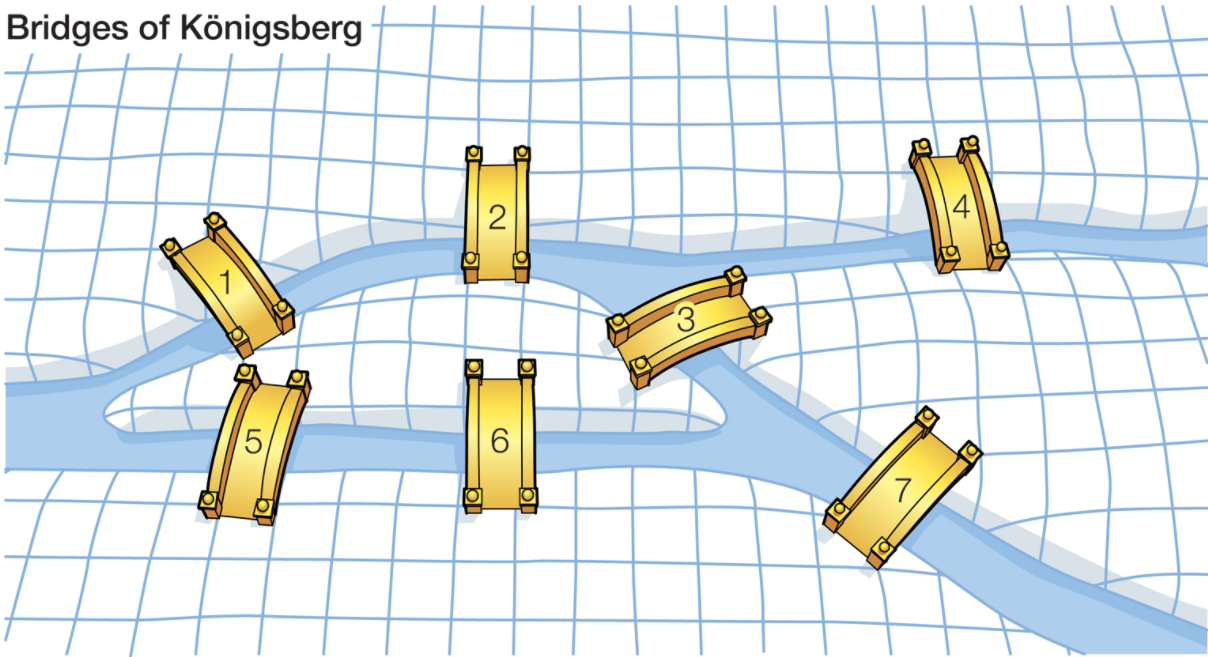
같은 다리를 두 번 이상 건너지 않으면서 7개의 다리들을 모두 건널 수 있을까?
불가능하다 by Leonhard Euler
강에 의해 나누어진 4조각의 땅을 ‘노드’로, 각 다리들을 ‘간선’으로 파악하여 문제를 해결.
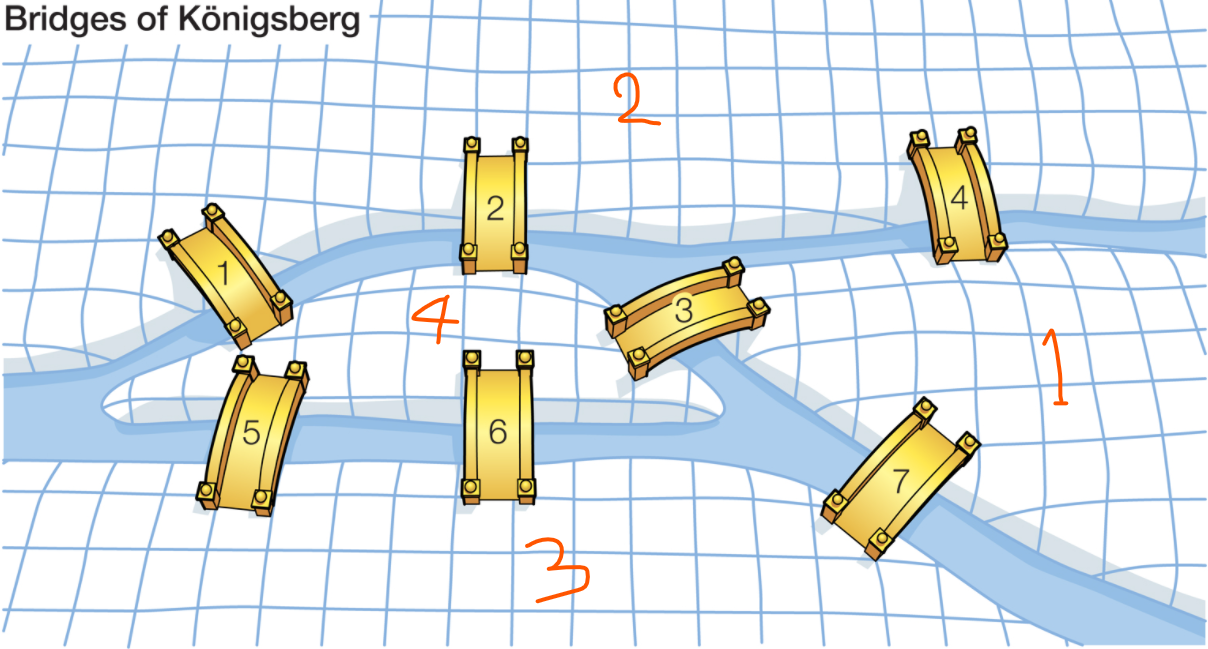
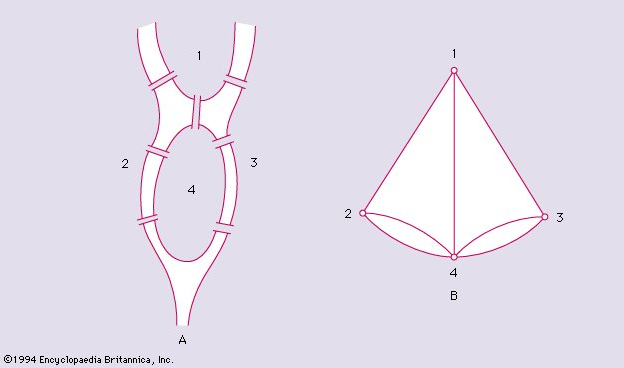
To confirm this, suppose that such a walk is possible. In a single encounter with a specific landmass, other than the initial or terminal one, two different bridges must be accounted for: one for entering the landmass and one for leaving it. Thus, each such landmass must serve as an endpoint of a number of bridges equaling twice the number of times it is encountered during the walk. Therefore, each landmass, with the possible exception of the initial and terminal ones if they are not identical, must serve as an endpoint of an even number of bridges. However, for the landmasses of Königsberg, ‘4’ is an endpoint of five bridges, and ‘1’, ‘2’, and ‘3’ are endpoints of three bridges. The walk is therefore impossible.
같은 다리를 두 번 이상 건너지 않으면서 모든 다리를 건널 수 있는 것이 가능하다고 가정하면, 출발 지점과 도착 지점을 제외한 다른 지점에는 들어오는 다리와 나가는 다리가 쌍으로(짝수로) 존재해야한다.
하지만 쾨니히스베르크 다리를 위 그림과 같은 그래프 모델로 나타내면 4번 지점에는 5개의 다리가 존재하고, 1,2,3번 지점에는 각 3개 씩의 다리가 존재하므로 해당 문제는 해결이 불가능하다.
오일러 경로(Eulerian Trail)와 오일러 회로(Eulerian Circuit)
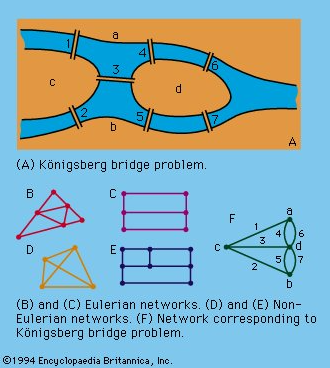
오일러 경로란 그래프에 존재하는 모든 간선(edge)을 정확히 한 번씩 통과하는 연속된 경로이다.
이때 처음 정점(vertex)으로 되돌아오는 경로는 오일러 회로가 된다.
정점에 연결된 간선의 수가 홀수인 정점이 2개 또는 0개 존재할 때 오일러 경로가 존재한다.
특히 그래프의 모든 정점에 연결된 간선의 개수가 짝수일 때, 즉 정점에 연결된 간선의 수가 홀수인 정점이 0개 일 때 오일러 회로가 존재한다.
해밀토니안 경로(Hamiltonian Path)
해밀토니안 경로란 그래프의 모든 정점(vertex)을 정확히 한 번씩 지나는 경로이다.
외판원 순회 문제(TSP, Traveling salesman problem)
1번부터 N번까지 번호가 매겨져 있는 도시들이 있고, 도시들 사이에는 길이 있다. (길이 없을 수도 있다) 이제 한 외판원이 어느 한 도시에서 출발해 N개의 도시를 모두 거쳐 다시 원래의 도시로 돌아오는 순회 여행 경로를 계획하려고 한다. 단, 한 번 갔던 도시로는 다시 갈 수 없다. (맨 마지막에 여행을 출발했던 도시로 돌아오는 것은 예외) 이런 여행 경로는 여러 가지가 있을 수 있는데, 가장 적은 비용을 들이는 여행 계획을 세우고자 한다.
지도 색칠하기
알고리즘: 그래프 색칠하기(m-coloring)(Backtracking 문제) 그래프 컬러링 문제 알아보기
Graph
As used in graph theory, the term graph does not refer to data charts, such as line graphs or bar graphs.
Instead, it refers to a set of vertices (that is, points or nodes) and of edges (or lines) that connect the vertices.
노드(N, Node)와 그 노드를 연결하는 간선(E, Edge)을 하나로 모아 놓은 자료 구조.
그래프의 종류
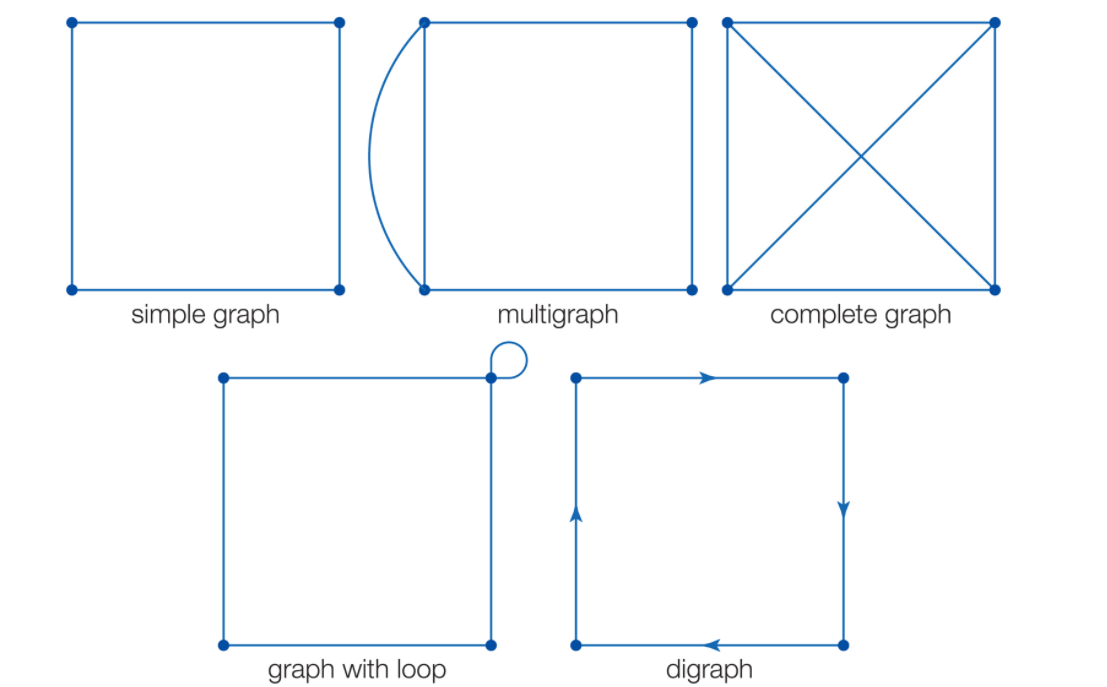
When any two vertices are joined by more than one edge, the graph is called a multigraph.
A graph without loops and with at most one edge between any two vertices is called a simple graph. Unless stated otherwise, graph is assumed to refer to a simple graph.
When each vertex is connected by an edge to every other vertex, the graph is called a complete graph.
When appropriate, a direction may be assigned to each edge to produce what is known as a directed graph, or digraph.
- 단순 그래프 (simple graph) : 두 정점사이에 하나의 간선만 존재하며, 루프가 없어야 한다. 달리 명시되지 않는 한, 단순 그래프를 말한다.
- 다중 그래프 (multigraph) : 두 정점 사이에 여러개의 간선이 존재한다.
- 완전 그래프 (complete graph) : 각 정점이 나머지 모든 정점과 연결되어 있다.
- 방향 그래프 (directed graph, digraph) : 간선에 방향성이 존재한다.
무방향 vs 방향 그래프
- 무방향 그래프(Undirected Graph)
- 간선을 통해 양방향으로 갈 수 있다.
- 정점 A와 B를 연결하는 간선은
(A,B)와 같이 표현할 수 있다. (A,B)는(B,A)와 같다.
- 방향 그래프(Directed Graph)
- 간선에 방향성이 존재한다.
- A->B로 갈 수 있는 간선은
<A,B>로 표현할 수 있다. <A,B>는<B,A>와 다르다.
연결 vs 비연결 그래프
- 연결 그래프(Connected Graph)
- 무방향 그래프에 있는 모든 정점쌍에 대해서 항상 경로가 존재한다. ※ Tree : 사이클을 가지지 않는 연결 그래프
- 비연결 그래프(Disconnected Graph)
- 무방향 그래프에서 특정 정점쌍 사이에 경로가 존재하지 않는 경우가 있다.
순환 vs 비순환 그래프
- 사이클(Cycle)
- 단순 경로의 시작 정점과 종료 정점이 동일하다. ※ 단순 경로(Simple Path) : 경로 중에서 반복되는 정점이 없는 경로
- 비순환 그래프(Acyclic Graph)
- 사이클이 없다.
무방향 완전 그래프 (Undirected Complete Graph)
- 정점의 개수가 n일 때 간선의 수는 n*(n-1)/2 이다.
가중치 그래프 (Weighted Graph)
- 간선에 비용이나 가중치가 할당된 그래프이다.
- ‘네트워크(Network)’ 라고도 한다.
그래프와 트리의 차이
| 그래프 | 트리 | |
|---|---|---|
| 정의 | 노드(Node)와 그 노드를 연결하는 간선(Edge)을 하나로 모아 놓은 자료 구조 | 그래프의 한 종류 DAG(Directed Acyclic Graph, 방향성이 있는 비순환 그래프)의 한 종류 |
| 방향성 | 방향(Directed), 무방향(Undirected) 그래프 모두 존재 | 방향성 존재(Directed) |
| 루트 노드 | 루트 노드의 개념이 없음 | 한 개의 루트 노드 존재 |
| 부모-자식 | - | 모든 자식 노드는 한 개의 부모 노드를 가지며, top-down 또는 bottom-up으로 이루어짐 |
| 모델 | 네트워크 모델 | 계층 모델 |
| 순회 | DFS, BFS | DFS, BFS(Pre-,In-,Post- order) |
| 간선 | 그래프에 따라 간선의 수가 다르며 간선이 없을 수도 있음 | 노드가 N개인 트리는 (N-1)개의 간선을 가짐 |
| 경로 | 다양한 경로 | 임의의 두 노드 간의 경로는 유일함 |
| 예시 | 지도, 네트워크, 교통망 등 | 이진 트리, 이진 탐색 트리, 균형 트리(AVL 트리, red-black 트리), 이진 힙(최대힙, 최소힙) 등 |
Graph and Algorithm
그래프와 경로
그래프 G(V,E) 는 어떤 자료나 개념을 표현하는 정점(vertex)들의 집합 V와 이들을 연결하는 간선(edge)들의 집합 E로 구성된 자료구조 이다.
그래프에서 경로(path)란 끝과 끝이 서로 연결된 간선들을 순서대로 나열한 것이다.
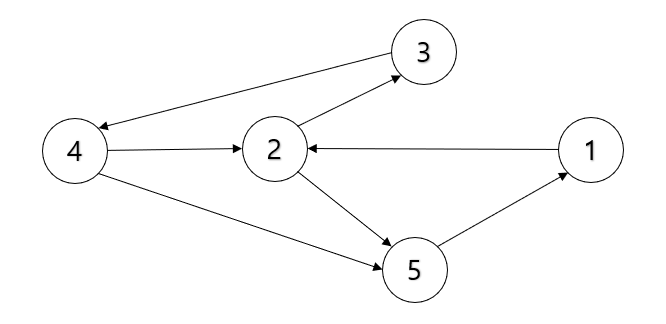
위 방향 그래프에서 <1,2>, <2,3>, <3,4>, <4,5>는 끝과 끝이 이어진 간선들이므로 하나의 경로를 이룬다.
해당 경로를 간단히 1-2-3-4-5 라고 표기하겠다.
경로 중 한 정점을 최대 한 번만 지나는 경로를 단순 경로(simple path)라고 부른다.
예를 들어 위 방향 그래프에서 경로 2-3-4-2-5는 2번 정점을 두 번 지나기 때문에 단순 경로가 아니다.
시작한 점에서 끝나는 경로를 사이클(cycle) 또는 회로(circuit)라고 부른다.
위 방향 그래프에서 경로 1-2-3-4-5-1은 사이클을 이룬다.
그래프의 사용 예
- 철도망의 안정성 분석 : 절단점 찾기 알고리즘
- 소셜 네트워크 분석
- 인터넷 전송 속도 계산 : 최소 스패닝 트리 (MST)
- 한 붓 그리기 : 오일러 경로
- 외환 거래
암시적 그래프 구조의 문제 예
그래프 같은 형태를 갖는 구조가 아니라도 그래프를 통해서 표현하면 쉽게 해결될 수 있는 문제들을 암시적 그래프(implicit graph)라고 부르기로 한다. (참고 : 프로그래밍 대회에서 배우는 알고리즘 문제해결전략 2권)
- 할 일 목록 정리 : 위상 정렬(topological sorting)
- 15-퍼즐 : A* 알고리즘
- 게임판 덮기 : 이분 그래프, 이분 매칭 알고리즘
- 회의실 배정 : 만족성 문제(satisfiability problem), 2-SAT, 그래프 강 결합성 문제
그래프 표현 방법
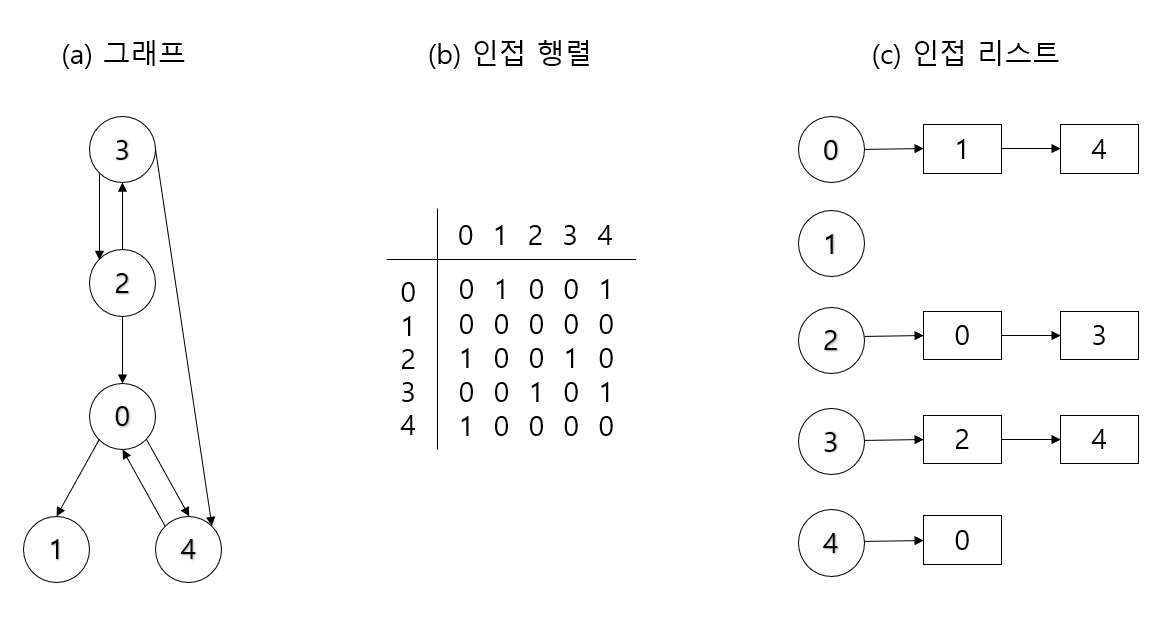
인접 행렬(adjacency matrix) vs 인접 리스트(adjacency list)
| 인접 행렬 | 인접 리스트 | |
|---|---|---|
| 구현 | int[][] adj |
ArrayList<ArrayList<Integer>> adj 또는 ArrayList<Integer>[] adj |
| 크기 | 정점의 개수에 따라 결정된다. |V|×|V| |
간선의 개수에 따라 결정된다. |V|+|E| |
| 장점 | 두 정점 u,v 이 주어질 때 간선 (u,v)가 존재하는지 확인하기 위해서 한 번의 배열 접근으로 가능하다. |
|V|개의 연결 리스트에 실제 간선의 수 만큼 O(|V|+|E|)의 공간만을 사용한다. |
| 단점 | 실제 간선의 개수와 상관없이 항상 O(|V|×|V|) 크기의 공간을 사용한다. |
두 정점이 주어질 때 연결 여부를 확인하려면 연결리스트 adj[u]를 처음부터 읽어가면서 일일이 확인해야 한다. |
| 결론 | 밀집 그래프(dense graph)에서 더 유리하다. | 희소 그래프(sparse graph)에서 더 유리하다. |
※ 밀집 그래프(dense graph) : 간선의 수가 |V|×|V|에 비례하는 그래프
※ 희소 그래프(sparse graph) : 간선의 수가 |V|×|V|에 비해 훨씬 적은 그래프
그래프의 어떤 표현 방식을 사용하느냐는 알고리즘의 시간복잡도에 영향을 주는 중요한 문제이다.
DFS를 이용한 그래프 탐색
- DFS 스패닝 트리
- 위상 정렬 (topological sorting)
- 오일러 트레일/서킷 (Eulerian Trail/Circuit)
- 이중 결합 컴포넌트
- 강결합 컴포넌트(Strongly Connected Components, SCC), 그래프의 압축(Condensation)
- 함의 그래프(implication graph)와 2-SAT (SAT 문제 : Boolean satisfiability problem)
위상정렬(Topological Sorting)
위상정렬(Topological Sorting) : 자세한 내용 - 작성 중
BFS를 이용한 그래프 탐색
- 최단 경로 알고리즘
최단 경로 알고리즘
다익스트라 (Dijkstra)
한 정점에서 출발하여 나머지 모든 정점까지의 최단경로를 구한다.
가중치가 음수인 경우 결과가 보장되지 않는다.
시간 복잡도 : O(|E|log|V|)
벨만-포드 (Bellman-Ford)
한 정점에서 출발하여 나머지 모든 정점까지의 최단경로를 구한다.
다익스트라보다 느리지만, 가중치가 음수인 경우에도 적용가능하다.
하지만 음수 가중치가 사이클을 이루고 있는 경우 정당성이 보장되지 않는다.
음수 사이클(negative cycle) 검사가 필요하다.
음수 사이클이 존재할 경우 방문했던 정점을 재방문했음에도 더 적은 비용이 계산될 수 있고,
사이클을 계속 돌다보면 최종적으로 최단 거리가 음의 무한대에 해당하는 정점이 발생하게된다.
1. 출발 노드를 설정한다.
2. 최단 거리 배열을 초기화한다.
3. 다음 과정을 (N-1)번 반복한다.
- 전체 간선 E개를 하나씩 확인한다. (다익스트라 알고리즘은 탐색하려는 노드에 연결된 간선만 검사한다)
- 각 간선을 거쳐 다른 노드로 가는 비용을 계산하여 최단 거리 배열을 갱신한다.
4. 음수 사이클 검사를 위해 3번 과정을 한 번 더 수행한다.
- 최단 거리 배열이 갱신되면 음수 사이클이 존재하는 것이다.
시간 복잡도 : O(VE)
플로이드 와샬 (Floyd Warshall)
모든 정점 쌍의 최단거리를 구할 수 있다.
가중치가 음수인 경우에도 적용가능하다.
void Floyd_Warshall() {
for(m=1; m<=N; m++)
for(s=1; s<=N; s++)
for(e=1; e<=N; e++)
if (d[s][e] > d[s][m] + d[m][e])
d[s][e] = d[s][m] + d[m][e];
}
플로이드 와샬 (Floyd Warshall) : 자세한 내용 - 작성 중
시간 복잡도 : O(V^3)
최소 스패닝 트리 (MST, Minimum Spanning Tree), 크루스칼 (Kruskal), 프림 (Prim)
- Spanning Tree : 무방향 연결 그래프(Undiredted and Connected Graph)에서 최소한의 간선으로 모든 정점을 포함하는 최소 연결 부분 그래프이다.
- MST, Minimum Spanning Tree : 가중치가 존재하는 무방향 연결 그래프(Weighted, Undiredted and Connected Graph)에서 가중치의 합을 최소로하는 스패닝트리이다.
- 크루스칼 (Kruskal) 알고리즘 : 그래프에서 가중치가 가장 작은 간선부터 방문하며 MST를 찾는 알고리즘이다.
- 프림 (Prim) 알고리즘 : 그래프에서 임의의 시작점으로부터 연결되는 가중치가 가장 작은 간선부터 방문하며 MST를 찾는 알고리즘이다.
최소 신장 트리(MST, Minimum Spanning Tree)와 크루스칼(Kruskal), 프림(Prim) 알고리즘 : 자세한 내용
이분 그래프와 이분 매칭 (bipartite matching)
이분 그래프 & 최대 이분 매칭 (Bipartite Graph & Maximum Bipartite Matching) 이분 그래프와 이분 매칭 (bipartite matching) : 자세한 내용 - 작성 중
Reference
- https://www.britannica.com/topic/graph-theory
- https://www.britannica.com/science/Konigsberg-bridge-problem
- https://www.britannica.com/science/traveling-salesman-problem
- https://gmlwjd9405.github.io/2018/08/13/data-structure-graph.html
- https://rain-bow.tistory.com/entry/%EC%98%A4%EC%9D%BC%EB%9F%AC-%EA%B2%BD%EB%A1%9C%EC%99%80-%ED%9A%8C%EB%A1%9CEulerian-trail-circuit
- 프로그래밍 대회에서 배우는 알고리즘 문제해결전략 2권