Hyebeen.So

최소 신장 트리(MST, Minimum Spanning Tree)와 크루스칼(Kruskal), 프림(Prim) 알고리즘

9 minute read

신장 트리(Spanning Tree)

A spanning tree is a subset of Graph G, which has all the vertices covered with minimum possible number of edges. Hence, a spanning tree does not have cycles and it cannot be disconnected..

By this definition, we can draw a conclusion that every connected and undirected Graph G has at least one spanning tree. A disconnected graph does not have any spanning tree, as it cannot be spanned to all its vertices.

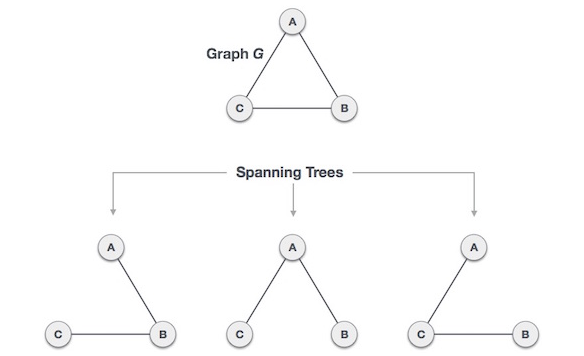
210625124715.png

n개의 노드(정점)를 가진 끊어지지 않은 양방향 그래프 G(every connected and undirected Graph G)에 대해서 Spanning Tree를 정의할 수 있다.

  • Spanning Tree는 그래프 G의 부분집합(subset)이다.
  • Spanning Tree는 그래프 G의 최소 연결 부분 그래프이다.
  • Spanning Tree는 그래프 G의 모든 정점을 포함한다.
  • Spanning Tree는 사이클이 존재하면 안된다.
    • Tree의 속성을 만족한다.
    • 간선을 하나라도 추가하면 사이클이 생긴다. (maximally acyclic, 최대 비순환)
  • Spanning Tree는 최소한의 간선으로 연결되어 있다. (minimally connected)
    • Spanning Tree는 n 개의 정점에 대해 (n-1) 개의 간선이 존재해야한다.
  • 하나의 그래프 G에는 여러 개의 Spanning Tree가 존재할 수 있다.
    • 최대 nn-2 개의 Spanning Tree가 존재할 수 있다.
      위 그림에서 n=3 이므로, 33-2=3 이라서, 3개의 Spanning Tree를 가질 수 있다.

최소 신장 트리(MST, Minimum Spanning Tree)

In a weighted graph, a minimum spanning tree is a spanning tree that has minimum weight than all other spanning trees of the same graph. In real-world situations, this weight can be measured as distance, congestion, traffic load or any arbitrary value denoted to the edges.

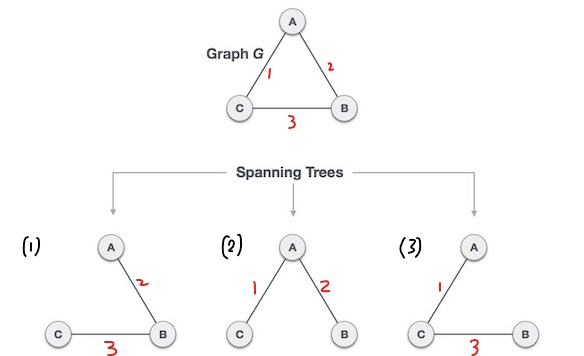
210625124715.png

그래프 G에 가중치를 추가했다. (weighted graph)
이 때, 최소한의 가중치를 갖는 (2)번 Spanning Tree가 MST, Minimum Spanning Tree이다.

Kruskal Algorithm

간선 리스트를 정렬하여 가중치가 가장 작은 간선부터 방문한다.

Kruskal’s algorithm to find the minimum cost spanning tree uses the greedy approach. This algorithm treats the graph as a forest and every node it has as an individual tree. A tree connects to another only and only if, it has the least cost among all available options and does not violate MST properties.

greedy approach(탐욕 알고리즘)를 사용하여 MST를 구하는 알고리즘이다.
Kruskal Algorithm은 각각의 노드를 individual tree로 취급한다.
각 트리는 연결된 모든 다른 트리 중 MST의 속성을 위반하지 않고 가중치가 가장 적은 트리를 선택하여 연결해 MST를 만든다.

예시

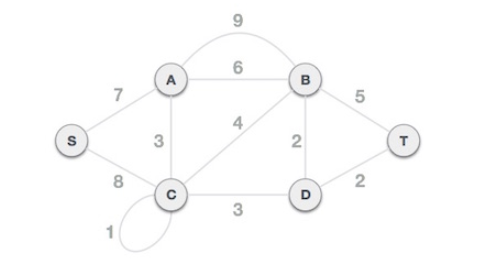
210625145304.png

1. 모든 loop와 평행 간선(parallel edge)을 제거한다. (Remove all loops and parallel edges)

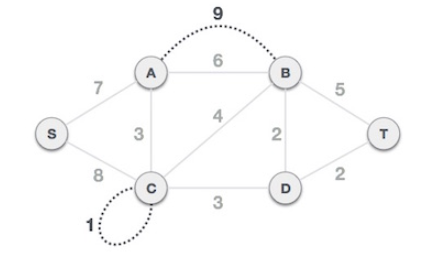
210625150728.png

210625150830.png

parallel edge을 제거 할 때는 가중치가 가장 적은 간선만 남겨둔다.

2. 가중치 오름차순으로 모든 간선을 정렬한다. (Arrange all edges in their increasing order of weight)

210625151005.png

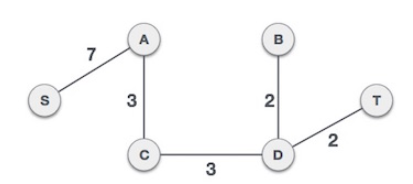
3. 가중치가 적은 간선부터 검사하여 MST에 추가한다. (Add the edge which has the least weightage)

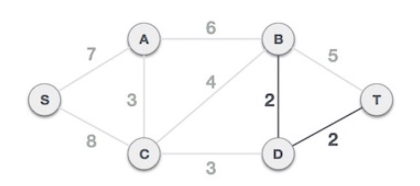
210625151335.png

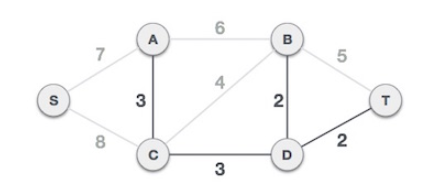
210625151347.png

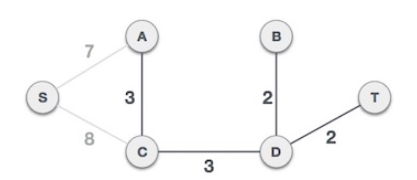
이 때, 새로운 추가할 간선이 기존 트리에 포함되는지 확인한다.
즉, loop가 생기는지 확인해야한다.

간선 (B-C,4)는 loop를 생성하므로 MST에 추가하지 않는다.

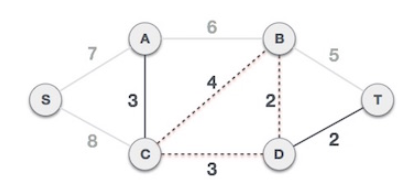
210625151545.png

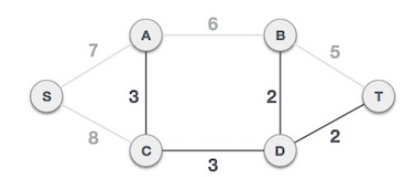
210625151605.png

210625151614.png

210625151640.png

마지막으로 간선 (S-A,7)을 추가하여 그래프의 모든 노드를 포함하는 MST를 완성했다.

시간복잡도

O(ElogV)

E : 그래프 G의 Edge의 개수 (간선)
V : 그래프 G의 Vertex의 개수 (노드)

구현 with Union Find(Cycle 검사), Priority Queue


import java.util.*;

public class Kruskal {

    public static int INF = Integer.MAX_VALUE/2;
    public static int N = 6;
    public static int[][] adj = {
            // A, B, C, D, S, T
/*A*/     {   0,  6, 3,INF, 7, INF},
/*B*/     {   6,  0, 4, 2, INF, 5},
/*C*/     {   3,  4, 0, 3,  8, INF},
/*D*/     { INF,  2, 3, 0, INF, 2},
/*S*/     {   7,INF, 8,INF, 0, INF},
/*T*/     { INF,  5,INF,2, INF,  0}
    };

    public static void main(String[] args) {
        System.out.println(kruskal(0));
    }

    /**
     *  union find
     */
    public static int[] p;

    public static int findSet(int x) {
        if(x==p[x]) return x;
        else return p[x] = findSet(p[x]);
    }
    public static void union(int x, int y) {
        p[findSet(y)] = findSet(x);
    }

    /**
     * kruskal
     */
    private static int kruskal(int start) {
        PriorityQueue<int[]> pq = new PriorityQueue<>((int[] o1, int[] o2)->(Integer.compare(o1[2], o2[2])));
        p = new int[N];
        makeSet();
        initPQ(pq);

        int sum = 0;
        int cnt = 0;
        while(!pq.isEmpty()) {
            int[] edge = pq.poll();
            if(isCycle(edge)) continue;
            printEdge(edge);
            sum += edge[2];
            if(++cnt == N-1) break;
            union(edge[0], edge[1]);
        }

        return sum;
    }

    private static boolean isCycle(int[] edge) {
        return findSet(edge[0]) == findSet(edge[1]);
    }

    private static void printEdge(int[] edge) {
        System.out.println(edge[0]+" - "+edge[1]+" , weight : "+edge[2]);
    }

    private static void initPQ(PriorityQueue<int[]> pq) {
        for(int i = 0; i < N-1; ++i) {
            for(int j = i+1; j < N; ++j) { // undirected Graph 이므로 절반만 offer
                if(adj[i][j]!=INF) pq.offer(new int[] {i,j, adj[i][j]});  // i - j, weight
            }
        }
    }

    private static void makeSet() {
        for(int i = 0; i < N; ++i) p[i] = i;
    }
}

Prim Algorithm

임의의 시작점으로부터 연결되는 가장 작은 가중치의 간선부터 방문한다.

Prim’s algorithm to find minimum cost spanning tree (as Kruskal’s algorithm) uses the greedy approach. Prim’s algorithm shares a similarity with the shortest path first algorithms.

Prim’s algorithm, in contrast with Kruskal’s algorithm, treats the nodes as a single tree and keeps on adding new nodes to the spanning tree from the given graph.

greedy approach(탐욕 알고리즘)를 사용하여 MST를 구하는 알고리즘이다.
최단 경로 알고리즘(the shortest path algorithm)과 유사하다.
prim 알고리즘은 kruskal 알고리즘과 달리 노드를 single tree로 취급하고 새로운 노드를 MST에 추가해나간다.

individual vs. single
https://hinative.com/en-US/questions/7576630
https://wikidiff.com/single/individual

kruskal 알고리즘에서는 edge가 선택되어도 각각의 노드는 개별적으로(individual) 존재하는 것으로 취급되며 각 노드의 root를 찾아 cycle을 검사한다. (union-find)
prim 알고리즘에서는 edge가 선택되면 포함된 노드들을 하나의(single) 노드처럼 취급한다.

예시

210625145304.png

1. 모든 loop와 평행 간선(parallel edge)을 제거한다. (Remove all loops and parallel edges)

210625150728.png

210625150830.png

parallel edge을 제거 할 때는 가중치가 가장 적은 간선만 남겨둔다.

2. 임의의 시작 노드를 root 노드로써 선택한다. (Choose any arbitrary node as root node)

해당 예시에서는 S노드를 root 노드로써 선택한다.
하지만, 임의의 모든 노드를 root 노드로써 시작할 수 있다.
Spanning Tree는 결국 그래프의 모든 노드를 포함하기 때문이다.

3. 확장되는 간선들 중 가중치가 가장 작은 것을 선택한다. (Check outgoing edges and select the one with less cost)

root 노드에 연결되지 않은 노드로 연결되는 간선들을 확장되는 간선이라고 한다. (outgoing edges)

root 노드 S에서 확장되는 간선들 (S-A,7), (S-C,8) 중에서 가중치가 더 작은 (S-A,7) 을 선택한다.

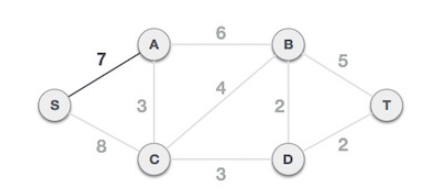
210625223143.png

이제 S-7-A가 하나의 노드로 취급된다.

S-7-A 에서 확장되는 간선들 (S-C,8), (A-C,3), (A-B,6) 중에서 가중치가 가장 작은 (A-C,3) 을 선택한다.

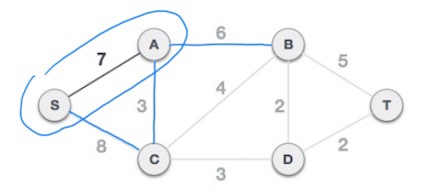
210625223143.png

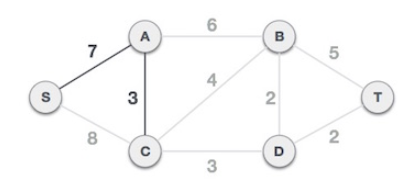
210625223155.png

이제 S-7-A-3-C 트리가 형성된다.
이 트리를 하나의 노드로 취급한다.

S-7-A-3-C 에서 확장되는 간선들 (A-B,6), (C-B,4), (C-D,3) 중에서 가중치가 가장 작은 (C-D,3) 을 선택한다.

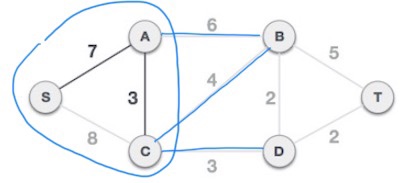
210625223143.png

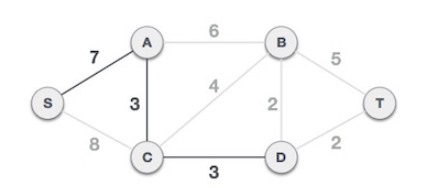
210625223208.png

이제 S-7-A-3-C-3-D 트리가 형성된다.
이 트리를 하나의 노드로 취급한다.

S-7-A-3-C-3-D 에서 확장되는 간선들 (A-B,6), (C-B,4), (D-B,2) 중에서 가중치가 가장 작은 (D-B,2) 을 선택한다.

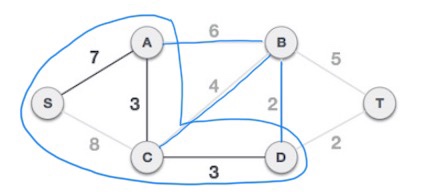
210625223143.png

다음으로 S-7-A-3-C-3-D-2-B 트리를 하나의 노드로 취급하고,
확장되는 간선들 (B-T,5), (D-T,2) 중에서 가중치가 더 작은 (D-T,2) 를 선택한다.

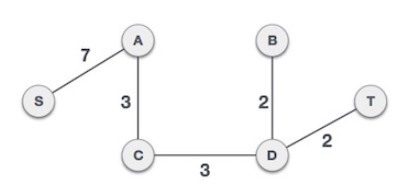
210625223219.png

kruskal과 prim 알고리즘 모두 동일한 MST를 만들었다.

시간복잡도

O(ElogV)

E : 그래프 G의 Edge의 개수 (간선)
V : 그래프 G의 Vertex의 개수 (노드)

구현 with Array

import java.util.*;

public class Prim {

    public static int INF = Integer.MAX_VALUE/2;
    public static int N = 6;
    public static int[][] adj = {
            // A, B, C, D, S, T
/*A*/     {   0,  6, 3,INF, 7, INF},
/*B*/     {   6,  0, 4, 2, INF, 5},
/*C*/     {   3,  4, 0, 3,  8, INF},
/*D*/     { INF,  2, 3, 0, INF, 2},
/*S*/     {   7,INF, 8,INF, 0, INF},
/*T*/     { INF,  5,INF,2, INF,  0}
    };
    private static int[] w;

    public static void main(String[] args) {
        System.out.println(prim(4));
    }

    private static int prim(int start) {
        w = new int[N];
        Arrays.fill(w, -1);
        w[start] = 0;

        for(int k = 0; k < N-1; ++k) {
            int minWeight = INF;
            int minVertax = 0;
            for(int i = 0; i < N; ++i) {
                if( w[i] < 0 ) continue;
                for(int j = 0; j < N; ++j) {
                    if( isVisited(j) ) continue;
                    if( minWeight > adj[i][j] ) {
                        minWeight = adj[i][j];
                        minVertax = j; // 최단 i->j
                        printEdge(new int[]{i,j, adj[i][j]});
                    }
                }
            }
            w[minVertax] = minWeight;
            printArrayW();
        }

        int sum = 0;

        for ( int i = 0; i < N; ++i)
            sum += w[i];

        return sum;
    }

    private static boolean isVisited(int idx) {
        return w[idx] >= 0;
    }
    private static void printEdge(int[] edge) {
        System.out.println(edge[0]+" - "+edge[1]+" , weight : "+edge[2]);
    }
    private static void printArrayW() {
        System.out.println("w : "+Arrays.toString(w));
    }
}

구현 with Priority Queue

import java.util.*;

public class Prim {

    public static int INF = Integer.MAX_VALUE/2;
    public static int N = 6;
    public static int[][] adj = {
            // A, B, C, D, S, T
/*A*/     {   0,  6, 3,INF, 7, INF},
/*B*/     {   6,  0, 4, 2, INF, 5},
/*C*/     {   3,  4, 0, 3,  8, INF},
/*D*/     { INF,  2, 3, 0, INF, 2},
/*S*/     {   7,INF, 8,INF, 0, INF},
/*T*/     { INF,  5,INF,2, INF,  0}
    };
    private static PriorityQueue<int[]> pq;

    public static void main(String[] args) {
        System.out.println(prim(4));
    }

    private static int prim(int start) {
        boolean[] visited = new boolean[N];
        visited[start] = true;
        pq = new PriorityQueue<>((int[] o1, int[] o2)->(Integer.compare(o1[1], o2[1])));
        for(int i = 0; i < N; ++i) {
            if(!visited[i] && adj[start][i] != INF) pq.offer(new int[] {i, adj[start][i]});
        }

        int sum = 0;
        int cnt = 0;
        while(!pq.isEmpty()) {
            printPQ();
            int[] current = pq.poll();
            int vertex = current[0];
            int weight = current[1];
            if(!visited[vertex]) {
                visited[vertex] = true;
                sum += weight;
                if(++cnt == N-1) break;
                printEdge(new int[]{vertex,weight});
                for(int i = 0; i < N; ++i) {
                    if(!visited[i] && adj[vertex][i] != INF) pq.offer(new int[] {i,adj[vertex][i]});
                }
            }
        }

        return sum;
    }

    private static void printPQ() {
        StringBuilder sb = new StringBuilder();
        sb.append("Priority Queue : ");
        Iterator<int[]> it = pq.iterator();
        while (it.hasNext()) {
            sb.append(Arrays.toString(it.next()));
        }
        System.out.println(sb.toString());
    }
    private static void printEdge(int[] edge) {
        System.out.println("vertex : " + edge[0]+" , weight : "+edge[1]);
    }
}

Solve Problem

백준 2887 행성터널

최대 10만개의 n에 대해서 n2 (10만 * 10만)의 연산 및 데이터가 발생하므로 메모리초과 문제를 신경써야한다.

n개의 행성들을 모두 연결시키면 안된다!

행성들의 x,y,z 좌표를 각각 정렬한다.
문제에 주어진 예시의 경우 다음과 같다.

5
11 -15 -15
14 -5 -15
-1 -1 -5
10 -4 -1
19 -4 19
idx 3 4 1 2 5
X -1 10 11 14 19
idx 1 2 4 5 3
Y -15 -5 -4 -4 -1
idx 1 2 3 4 5
Z -15 -15 -5 -1 19

X좌표 기준으로 3번 행성에 대해서 3-1, 3-2, 3-4, 3-5 의 모든 간선을 계산할 필요없이 정렬된 순서에 따른 (3-4, 11) 의 간선이 가장 가중치가 작다는 것을 알 수 있다.

이런식으로 X,Y,Z 좌표마다 계산된 간선 (n-1)개를 후보에 두면 최대 3*(n-1)개의 간선에 대해서 연산이 이루어진다.

그 다음은 Kruskal 알고리즘을 이용하여 MST를 구했다.

import java.io.*;
import java.util.*;

public class Main_bj_2887_행성터널 {
    private static int n;
    private static PriorityQueue<int[]> pqX;
    private static PriorityQueue<int[]> pqY;
    private static PriorityQueue<int[]> pqZ;
    private static PriorityQueue<int[]> pq;
    private static int[] p;

    public static void main(String[] args) throws IOException {
        System.setIn(new FileInputStream("solveProblem/res/Main_bj_28847_행성터널.txt"));
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));

        n = Integer.parseInt(br.readLine());

        pqX = new PriorityQueue<>((int[] o1, int[] o2) -> (Integer.compare(o1[1], o2[1])));
        pqY = new PriorityQueue<>((int[] o1, int[] o2) -> (Integer.compare(o1[1], o2[1])));
        pqZ = new PriorityQueue<>((int[] o1, int[] o2) -> (Integer.compare(o1[1], o2[1])));
        for (int i = 0; i < n; i++) {
            StringTokenizer st = new StringTokenizer(br.readLine());
            pqX.offer(new int[]{i, Integer.parseInt(st.nextToken())});
            pqY.offer(new int[]{i, Integer.parseInt(st.nextToken())});
            pqZ.offer(new int[]{i, Integer.parseInt(st.nextToken())});
        }

        System.out.println(kruskal());

        br.close();
    }

    private static int kruskal() {
        p = new int[n];
        makeSet();

        pq = new PriorityQueue<>((int[] o1, int[] o2) -> (Integer.compare(o1[2], o2[2])));
        initPQ();

        int sum = 0;
        int cnt = 0;
        while (!pq.isEmpty()){
            int[] edge = pq.poll();
            if(isCycle(edge)) continue;
            sum += edge[2];
            union(edge[0], edge[1]);
            if(cnt++ == n-1) break;
        }

        return sum;
    }

    private static boolean isCycle(int[] edge) {
        return find(edge[0]) == find(edge[1]);
    }

    private static void initPQ() {
        int[] current = pqX.poll();
        while (!pqX.isEmpty()) {
            int[] next = pqX.poll();
            pq.offer(new int[]{current[0], next[0], Math.abs(current[1] - next[1])});
            current = next;
        }

        current = pqY.poll();
        while (!pqY.isEmpty()) {
            int[] next = pqY.poll();
            pq.offer(new int[]{current[0], next[0], Math.abs(current[1] - next[1])});
            current = next;
        }

        current = pqZ.poll();
        while (!pqZ.isEmpty()) {
            int[] next = pqZ.poll();
            pq.offer(new int[]{current[0], next[0], Math.abs(current[1] - next[1])});
            current = next;
        }
    }

    private static void makeSet() {
        for(int i = 0; i < n; i++) p[i] = i;
    }

    private static int find(int x) {
        if(p[x] == x) return x;
        return p[x] = find(p[x]);
    }

    private static int union(int x, int y) {
        return p[find(y)] = find(x);
    }

}


Reference

Tutorialspoint - Spanning Tree

Tutorialspoint - Kruskal Algorithm

Tutorialspoint - Prim Algorithm

You may also enjoy

AOP

6 minute read

Aspect-Oriented Programming (AOP)